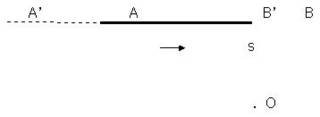
On the observation of a moving object.

As light needs time to travel from one point to an other, the only images we are able to perceive come from the past. The moon we see in the sky is not the moon as it is, it’s the moon as it was about a second ago. For everyday objects, the fact that we only perceive their past situations is of no importance. However, for very large objects or for those that are moving very fast, what is perceived is misleading.

1. Let’s suppose that a rod AB is moving lengthwise, from left to right at a constant speed s, in front of an observer placed at O.

fig 1d


A’ and B’ are the past images of A and B perceived simultaneously by the observer.

As A’ is farther from O than is B’, for both images to reach O together the image of A’ must come from a more distant past than the image of B’. This means that A’ is farther behind A, than B’ is behind B.

If A’O > B’O, then A’A > B’B
But also :
If A’O = B’O, then A’A = B’B
If B’O > A’O, then B’B > A’A

Furthermore A’B’ + B’B = AB + A’A

So A’B’ = AB + A’A - B’B

And if A’O > B’O (A’A > B’B), then A’B’ > AB
If A’O = B’O (A’A = B’B), then A’B’ = AB

If B’O > A’O (B’B > A’A), then AB > A’B’

As the observer can only perceive A’B’, the past positions of A and B, the rod first appears to be longer than it really is, then it appears shorter, with an intermediary stage when the apparent length (A’B’) and the real length (AB) are equal.

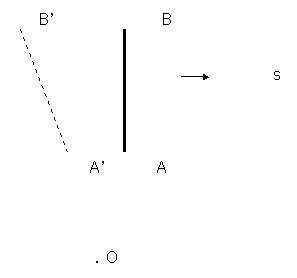
2. Let’s now suppose that the rod AB is moving sideways, instead of lengthwise.

fig 1d

As B’ is farther from O than A’ is, for both images to reach O together, the image of B’ must come from a more distant past than the image of A’. This means that B’ is farther behind B, than A’ is behind A.
In this case, for all positions of AB, B’O > A’O (B’B > A’A)
This means that A’B’ is always longer than AB. However, this extra length appears to increase as the rod gets closer and to shrink as the rod goes off into the distance. The greatest length of A’B’ is perceived when A’O is at its shortest. That is, when B’O - A’O is at its maximum.

3. We can also suppose that the rod AB is at rest and the observer O moves past it from left to right at a constant speed s.


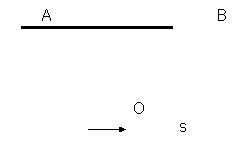
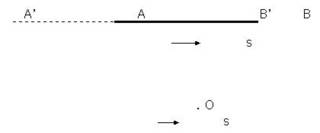
fig 1d

In this case, A and B are always at the same place. Their past, present and future positions are unchanged. The observer perceives past images of A and B that are identical in position to A and B. Which means that there is no difference between his perception of AB and AB’s reality.


4. In the real universe (as opposed to the imaginary universe we have described so far), nothing is at rest. Everything is in motion, either together or separately.
Let’s suppose that both the rod AB and the observer O are moving from left to right at a constant speed s.


fig 1d

In this case, the observer is moving away from the image A’ and toward the image B’. This lengthens the distance A’O and shortens the distance B’O. Which means that A’ comes from a more distant past and is farther behind A than was suggested above (1). And B’ is nearer to B. This in turn means that A’B’ is always that much longer, wherever the observer places himself and notwithstanding whether the perceived image of A’B’ is longer or shorter than AB. This finally means that the perceived rod A’B’ is not equal in length to AB when A’O = B’O. To perceive A’B’ = AB, the observer must move to the left, so that B’O > A’O

An experiment with sound.

Let's suppose that a plane is flying past an observer at half the speed of sound.
Mark off twenty equal spaces on a sheet of paper, ten before the observer and ten after. The plane covers this distance at a constant speed.But where is the plane, when the observer hears the sound it's making?
The sound made ten spaces away is heard when the plane is half that distance away (5). The sound made nine spaces away is heard when the plane is half that distance away (4.5). Etc.
The plane flies towards the observer and then away from him. Here, the sound made by the plane one space away is heard when the plane is one and a half spaces away. Two spaces corresponds to three, etc.
As the plane approaches the observer at half the speed of sound, the sound it makes during a flight of ten spaces is heard during a flightof only five spaces. The sound is heard at twice the speed it was made.
As the plane goes away at the same constant speed, the sound it makes during ten spaces is heard during fifteen spaces. The sound is heard at two thirds the speed it was made.
Sound speeded up is pitched higher.
Sound slowed down is pitched lower.
If you do the same experiment with a plane flying at the speed ofsound and with one flying faster than sound, you'll find that these results also coincide with the observed (heard) phenomena.